Question

Solve the radical equation. square root 6n-11= n – 3 Which solution is extraneous? A.)2

B.)There are no extraneous solutions to the equation.
C.)7
D.)10

Answer 1

d 10 right????????????:

Answer 2

ANSWER


D) 10

Step-by-step explanation

We want to solve the radical equation,


`√(6n - 11) = n - 3`

Square both sides,




`6n - 11 = (n - 3) ^(2)`

Expand brackets on right hand side,


`6n - 11 = {n}^(2) - 6n + 9`

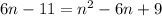
Rewrite in general quadratic equation form,


`{n}^(2) - 12n + 20 = 0`

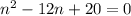
Factor to obtain,


`(n - 2)(n - 10) = 0`

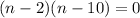
Apply the zero product principle to get,


`n = 2 \: or \: n = 10`


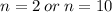
We put n=2 into the equation to get,


`√(6(2) - 11) = 2 - 3`



`1 = - 1`


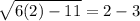
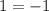
This statement is false, hence 2 is an extraneous solution


We put n=10, to get


`√(6(10) - 11) = 10 - 3`



`√(49) = 7`



`7 = 7`


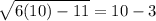
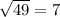
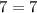
This is true, hence the only solution is

`n = 10`