Question

Find tan (a+B), given cot a= -3/4 , csc B= 25/24 , 90° < a < 180° , 90°< B < 180°

Answer 1

tan(a + B) =
`(4)/(3)`

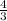
Explanation:

cot(a) =
`-(3)/(4)`

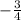
Therefore, tan(a) =
`-(4)/(3)`

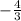
cosec(B) =
`(25)/(24)`

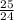
Since, 1 + cot²(B) = cosec²(B)

1 + cot²(B) =
`((25)/(24))^(2)`

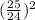
cot²(B) =
`(625)/(576)-1`

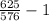
cot(B) =
`\sqrt{(49)/(576)}`

=
`\pm (7)/(24)`

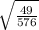
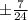
tan(B) =
`\pm (24)/(7)`

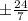
Since, tan and cot of an angle is negative in II quadrant,

Therefore, tan(B) =
`-(24)/(7)`

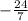
Since, tan(a + B) =
`\frac{\text{tan}(a)+\text{tan}(B)}{1-\text{tan(a)tan(B)}}`

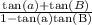
By substituting the values in the identity,

tan(a + B) =
`(-(4)/(3)-(24)/(7))/(1-(-(4)/(3))(-(24)/(7)))`

=
`(-(28)/(21)-(72)/(21))/(1-((32)/(7)))`

=
`(-(100)/(21) )/((7-32)/(7) )`

=
`(100)/(21)* (7)/(25)`

=
`(4)/(3)`

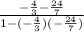
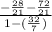
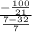
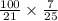
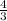
Therefore, tan(a + B) =
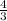`(4)/(3)` is the answer.