Question

Write a function in the form y=mx+b for the line that contains the points (-6.4, -2.6 )and (5.2,9)

Answer 1

The function in the form y = mx+b will be:

y = x + 3.8

Explanation:

We know that the slope-intercept form of the line equation

`y = mx+b`

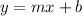
where

• m is the slope

• b is the y-intercept

Given the points

• (-6.4, -2.6)

• (5.2, 9)

Determining the slope between (-6.4, -2.6 )and (5.2,9)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-6.4,\:-2.6\right),\:\left(x_2,\:y_2\right)=\left(5.2,\:9\right)`

`m=(9-\left(-2.6\right))/(5.2-\left(-6.4\right))`

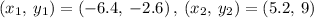
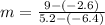
Refine

`m=1`

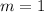
substituting (5.2, 9) and m = 1 in the slope-intercept form of the line equation

y = mx+b

9 = 1(5.2) + b

b + 5.2 = 9

b = 9 - 5.2

b = 3.8

Therefore, the value of x = 3.8

now substituting b = 3.8 and m = 1 in the slope-intercept form of the line equation

y = mx+b

y = 1(x) + 3.8

y = x + 3.8

Therefore, the function in the form y = mx+b will be:

y = x + 3.8