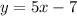Answer:
Step-by-step explanation:
Using slope-intercept form:
The equation of line is given by:
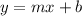 .....[1]
.....[1]
where,
m is the slope of the line
b is the y-intercept.
As per the statement:
The points (3, 8) and (2, 3) fall on a particular line.
Using slope(m) formula:
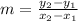
Substitute the given points we have;
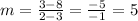
⇒m = 5
Put m = 5 in [1] we have;
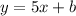
Substitute the point (3, 8) we have;
8 = 5(3)+b
8 = 15+b
Subtract 15 from both sides we have;
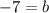
or
b = -7
Then we have;
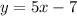
Therefore, the equation of line in slope intercept form is,