Question

Last​ year, a person wrote 134134 checks. let the random variable x represent the number of checks he wrote in one​ day, and assume that it has a poisson distribution. what is the mean number of checks written per​ day? what is the standard​ deviation? what is the​ variance?

Answer 1

Answers:

(a) mean = 367.24
(b) standard deviation = 19.17
(c) variance = 367.24

Explanations:

(a) Let
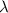
`\lambda` = rate parameter of parameter, which is the rate at which the number of checks are made in one day.

Since the person wrote 134,134 checks in last year, we can compute the rate parameter by dividing 134,134 by 365.251 because there are 365.251 days in a year. So,


`\lambda = (134,134)/(365.251) \approx 367.237872`

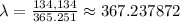
Since the number of checks in one day follows a Poisson distribution, the mean number of checks in one day is the rate parameter
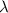
`\lambda`. Hence, the mean number of checks in one day is approximately 367.24.

(b) Since the number of checks in one day follows a Poisson distribution, the variance is equal to the rate parameter. Since the standard deviation is the square root of variance, the standard deviation is the square root of the rate parameter. In terms of equations,


`\text{standard deviation} \\ = √(\lambda) \\ = \sqrt{(134,134)/(365.251)} \\ \boxed{\text{standard deviation} \approx 19.17}`

(c) As mentioned in (b), because the number of checks written per day follows poisson distribution, the variance is equal to the rate parameter. Since the rate parameter is approximately 367.24, therefore the variance is approximately 367.24.