Question

The half-life of a medication is 6 hours. How can I find the rate of decay to the nearest hundredth?

Answer 1

The decay rate of the medication is approximately
`0.116\,(1)/(h)`.

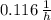Explanation:

If we know that amount of medication decays exponentially, this amount is represented by the following expression:

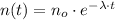`n(t) = n_(o)\cdot e^(-\lambda\cdot t)` (1)

Where:

`n_(o)` - Initial amount of medication.

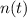`n(t)` - Current amount of medication.

`t` - Time, measured in hours.

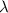`\lambda` - Decay rate, measured in
`(1)/(h)`.

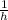In addition, the decay rate is determined by the following formula:

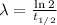`\lambda = (\ln 2)/(t_(1/2))` (2)

If we know that
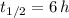`t_(1/2) = 6\,h`, then the decay rate is:

`\lambda = (\ln 2)/(6\,h)`

`\lambda \approx 0.116\,(1)/(h)`

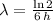
The decay rate of the medication is approximately
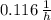`0.116\,(1)/(h)`.