Question

Circle Y is shown. What is the area of the shaded part of the circle?

Answer 1

This question will employ the use of the formula for the area, A, of a sector of any circle. The formula is as:

`A=(\theta)/(360^(\circ))* \pi r^2`

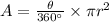
Where
`\theta` is the angle subtended by the required sector. In our case, the sector is the shaded region and we need to find the angle of that shaded region. We know that the total angle of a circle is 360 degrees and the unshaded region subtends an angle of 75 degrees. Thus, the value of
`\theta` is calculated to be:

`\theta=360^(\circ)-75^(\circ)=285^(\circ)`

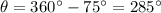
r is the radius of the circle which in our case is 9 cm.

Thus, the area of the shaded region is:

`A=(285)/(360)* \pi* 9^2=(19)/(24)\pi* 81 =(19* 81)/(24)\pi`

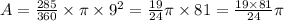
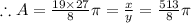`\therefore A=(19* 27)/(8)\pi=(x)/(y) =(513)/(8)\pi` cm^2

Thus, Option D is the correct option.