Question

Solve for x 3x−91>−87 OR 21x−17>25

Answer 1

The solution is
`x>(4)/(3)`

Explanation:

A compound inequality is an inequality that combines two simple inequalities.

We want to solve for x the following compound inequality

`3x-91>-87 \:{OR} \:{21x-17>25}`

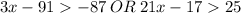
Solving the first inequality for x, we get:

`3x-91+91>-87+91\\\\3x>4\\\\x>(4)/(3)`

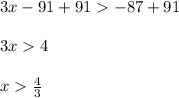
Solving the second inequality for x, we get:

`21x-17+17>25+17\\\\21x>42\\\\x>2`

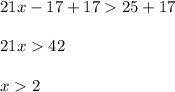
So our compound inequality can be expressed as the simple inequality:

`x>(4)/(3)`

The graph of a compound inequality with an "or" represents the union of the graphs of the inequalities. A number is a solution to the compound inequality if the number is a solution to at least one of the inequalities.

Graphically, we get

Answer 2

x > 4/3

Explanation:

The first inequality can be solved this way ...

3x -91 > -87

3x > 4 . . . . . . . add 91

x > 4/3 . . . . . . divide by 3

__

The second inequality has solution ...

21x -17 > 25

21x > 42 . . . . . . add 17

x > 2 . . . . . . . . . divide by 21

__

The solution set is the union of these overlapping solutions, so will be equal to the first solution:

x > 4/3