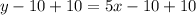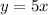Question:
Find the constant of proportionality k. Then write an equation for the relationship between x and y
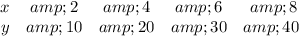
Answer:
(a)
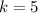
(b)
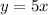
Explanation:
Given
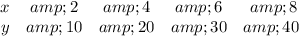
Solving (a): The constant of proportionality:
Pick any two corresponding x and y values
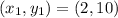
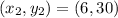
The constant of proportionality k is:
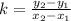
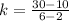
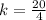
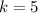
Solving (b): The equation
In (a), we have:
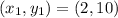
k can also be expressed as:
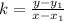
Substitute values for x1, y1 and k
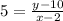
Cross multiply:
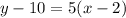
Open bracket
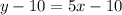
Add 10 to both sides