Question

Find all solutions in the interval [0, 2π).

2 sin2x = sin x


x = pi divided by three. , two pi divided by three.
x = pi divided by two. , three pi divided by two. , pi divided by three. , two pi divided by three.
x = 0, π, pi divided by six , five pi divided by six
x = pi divided by six , five pi divided by six

Answer 1

bro, use your trig identities

`sin2x=2sinxcosx`
So,

`2sin2x=sinx`

`4sinxcosx=sinx`

`4sinxcosx-sinx=0`

`sinx(4cosx-1)=0`

`sinx=0` &
`4cosx=1`

x = 0, π

x = acos(1/4)=1.32

Answer 2

All solutions of the equation are
`{0,\pi, \arccos(1)/(4), 2\pi-\arccos(1)/(4)}`.

Explanation:

I am assuming that the equation is
`2\sin 2x-\sin x = 0`.

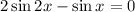Notice that the equation can be written as
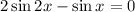`2\sin 2x-\sin x = 0`. Always is better to have the equations equated to zero. The next step is to use some trigonometrical identities, in this case we will use

`\sin(2x) = 2\sin x\cos x.`

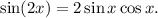
Hence, the equation becomes

`4\sin x\cos x-\sin x =0.`

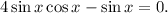
Extracting the common factor:

`\sin x(4\cos x -1)=0.`

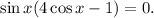
Then, we need to solve two simpler equations:

`\sin x =0` and
`4\cos x-1=0`

Let us start with the first one. The sinus is zero in 0,
`\pi` and
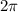`2\pi`, but this last point isn't included in the interval. Then, all the solutions in
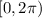`[0,2\pi)` are {0,
`\pi`}.

In the second equation we have
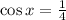`\cos x=(1)/(4)`, so
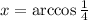`x=\arccos(1)/(4)`. Now, notice that this solution is in the first quadrant, and we are looking for all the solutions in
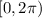`[0,2\pi)`, then we need to include the co-terminal angle in the fourth quadrant. Using the reduction formulas, the other solution is
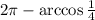`2\pi-\arccos(1)/(4)`.