Answer:
(f/g)(x) = Quantity five x plus three divided by six x minus five.domain x ≠ Five over six.
Step-by-step explanation:
Given functions,
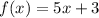


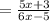 ( By substitution )
( By substitution )
Let
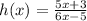
Which is the rational function,
Since, a rational function is defined for all real number except those for which denominator = 0,
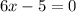
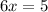
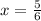
Thus, h(x) is defined on all real numbers except 5/6,
Hence, domain of
 is {x| x ≠
is {x| x ≠
 }
}