Question

Radical functions. please help me!

Answer 1

These are 8 questions and 8 answers:

1) Quesion 1:

9+√2
---------
4 - √7

Answer: the third option:

36 + 9√7 + 4√2 + √14
-----------------------------
9

Explanation:

Multiply both numerator and denominator by the conjugate of the denominator.

The conjugate of 4 - √7 = 4 + √7

=>


`(9+ √(2) )/(4- √(7) ) . (4+ √(7) )/(4+ √(7) ) = ((9)(4)+9 √(7)+4 √(2) + √(2) . √(7) )/((4)^2-( √(7))^2 ) =`


`= (36+9 √(7) +4 √(2) + √(14) )/(16-7)`

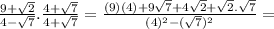
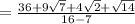2) Question 2: sum


`5x (\sqrt[3]{x^2y})+2( \sqrt[3]{x^5y})`

Answer: fourth option


`7x( \sqrt[3]{x^2y} )`

Step-by-step explanation:

Take x^5 out of the second radical which will result in a like term of the first radical:


`5x( \sqrt[3]{x^2y} )+2( \sqrt[3]{x^5y}) =5x( \sqrt[3]{x^2y} )+2x( \sqrt[3]{x^2y})=7x( \sqrt[3]{x^2y})`

which is the fourth option

3) Question 3. Which expression is equivalent to:


`\frac{ √(10) }{ \sqrt[4]{8} }`

Answer: the first option

Explanation


`\frac{ √(10) }{ \sqrt[4]{8} } = \frac{ \sqrt[4]{10^2} }{ \sqrt[4]{8} } = \frac{ \sqrt[4]{100} }{ \sqrt[4]{8} } . \frac{ \sqrt[4]{8^3} }{ \sqrt[4]{8^3} } = \frac{ \sqrt[4]{(100)(512)} }{8} = \frac{ \sqrt[4]{51200} }{8} = \frac{4 \sqrt[4]{200} }{8} = \frac{ \sqrt[4]{200} }{2}`

4) Question 4 What is the simplest form?

Answer: the second option

Step-by-step explanation:


`\sqrt[4]{81x^8y^5}=x^2 y\sqrt[4]{3^4y} =3x^2y \sqrt[4]{y}`

5) Question 5 Product

Answer: the fourth option:


`image`


`=16x^2(5x^2)+16x^4( √(30) )+4x^4(6)=80x^4+16x^4 √(30) +24x^4=`


`=104x^4+16x^4 √(30)`

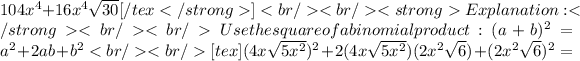
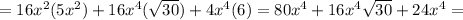
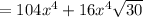
which is the fourth option.

6) Question 6 Product

Answer: fourth option

Step-by-step explanation:


`\sqrt[3]{16x^7} . \sqrt[3]{12x^9} = \sqrt[3]{2^4.2^2.3x^7x^9} = \sqrt[3]{2^6.3.x^(16)}=2^2 x^5 \sqrt[3]{3x} =4 x^5\sqrt[3]{3x}`

which is the fourth option.

7) Question 7. Simplified form of 2√18 + 3√2 + √162

Answer: 18√2

Step-by-step explanation:


`2 √(18)+3 √(2) + √(162)=2(3) √(2) + 3 √(2) +9 √(2) =18 √(2)`

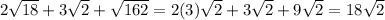
which is the second option.

8) Question 8 which function is undefined for x = 0.

Answer: second option y = √ (x - 2)

Explanation.

The square root function is not defined for negative values.

When x = 0, x - 2 = -2, whose square root is not defined.

Therefore, the square root of x - 2 is not defined for x = 0.