Question

Given an exponential function for compounding interest, A(x) = P(.91)^x, what is the rate of change?

A. −0.09%
B. −9%
C. 0.91%
D. 91%

Answer 1

The confirmed correct answer is -9%. Trust me.

Answer 2

Option B = -9%

Explanation:

Given : Given an exponential function for compounding interest,
`A(x) = P(.91)^x`

To find : What is the rate of change?

Solution :

The general form of the exponential function is
`f(x)=a(1+r)^x`

Where,

r is the rate of change

if r> 1 then it is growth rate

if r< 1 then it is decay rate.

Comparing given function with exponential function,

`A(x) = P(.91)^x`

`1+r=0.91`

`r=0.91-1`

`r=−0.09`

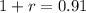
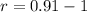
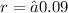
It is a decay rate.

Convert into percentage, multiply with 100

`-0.09* 100=-9\%`

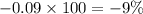
Therefore, Option B is correct.

The rate of change is -9%.