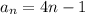Question

Write a recursive rule and an explicit rule for the
sequence
3,7,11,15

Answer 1

The Recursive formula for the sequence is:

aₙ = aₙ₋₁ + d

The Explicit formula for the sequence is:

`a_n=4n-1`

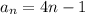
Explanation:

Given the sequence

3,7,11,15

Here:

a₁ = 3

computing the differences of all the adjacent terms

7 - 3 = 4, 11 - 7 = 4, 15 - 11 = 4

The difference between all the adjacent terms is the same and equal to

d = 4

We know that a recursive formula basically defines each term of a sequence using the previous term(s).

The recursive formula of the Arithmetic sequence always involves the first term.

a₁ = 3

We know that, in the Arithmetic sequence, every next term can be obtained by adding the common difference and the preceding term.

so

The recursive formula of the sequence is:

aₙ = aₙ₋₁ + d

substitute n = 2 to find the 2nd term

a₂ = a₂₋₁ + d

a₂ = a₁+ d

substitute a₁ = 3 and d = 4

a₂ = 3 + 4

a₂ = 7

Thus, the recursive formula for the sequence 3,7,11,15 is:

aₙ = aₙ₋₁ + d

An explicit rule for the sequence

Given the sequence

3,7,11,15

We already know that

a₁ = 3

d = 4

An arithmetic sequence has a constant difference 'd' and is defined by

`a_n=a_1+\left(n-1\right)d`

substituting a₁ = 3 and d = 4

`a_n=4\left(n-1\right)+3`

`a_n=4n-4+3`

`a_n=4n-1`

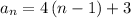
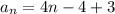
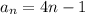
Therefore, an explicit rule for the sequence

`a_n=4n-1`