For a better understanding of the solution provided here please go through the graph in the attachment. Please note that the solution provided here will be an approximate solution.
In the graph, the x axis is the number of months. 1 is January, 2 is February, so on and so forth.
The y axis is the expected number of daylight hours in those months. Each point has been depicted in the graph as shown.
Now, when we look at the graph we notice a pattern. The graph is nearly a cosine graph. Thus the equation that will best model the data will be an equation of the cosine form and will look like:
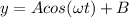
where symbols have their usual meanings.
Let us find each term now:
We know that in December, the expected number of daylight hours is 9.25 hours. Thus, let us assume that the expected number of daylight hours in previous December was 9.25 hours too.
With this assumption let us proceed.
Amplitude=
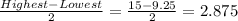
The Vertical Shift Up is B=
Also, the frequency can be calculated as:
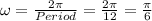
Thus, plugging in all the values, the final equation will be:
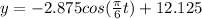....(Equation 1)
The negative value of A suggests that the function starts below the horizontal y=12.125 line.
The above is the (Equation 1) that best models the given data.
Now, to find the expected number of daylight hours in March 2020, we just have to find the value of the time, t from January 2015 to March 2020.
Now, we know that each year has 12 months. So, 5 years from start of 2015 to end of 2019 will have 12 x 5=60 months. We need to add to this the first three months of the year 2020 to take us till March 2020. Thus, the value of t from January 2015 to March 2020 is 63.
Now, let us use the (Equation 1) to find the value of expected number of daylight in March 2020 by plugging in t=63 in it.
Thus,
Expected number of daylight in March 2020 is:
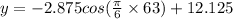
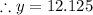hours.