The holes in this function are the points where you can cancel factors from the numerator and denominator.
We factor the function.
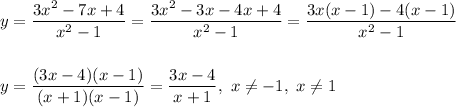
We canceled (x-1) from the numerator and denominator, so when this factor is equal to zero, there is a hole on the graph, that is, at the point
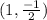
.