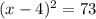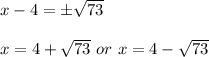Question

Use completing the square to solve for x in the equation (x-12)(x+4)=9.

a. x = –1 or 15
b. x = 1 or 7
c. x=4+√41
d. x=4+√73

Answer 1

The correct answer is

D

Answer 2

For a quadratic of the form
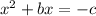
`x^2+bx=-c`, we can solve by completing the square.

First, we must expand the expression and convert it to the form above.


`(x-12)(x+4)=9\\x^2+4x-12x-48=9\\x^2-8x=57`

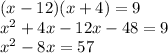
Completing the square is like forcing a quadratic to be factored like a perfect square trinomial. To do so, we add the square of half of the coefficient b,
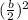
`( (b)/(2))^2`, to both sides of the equation.


`x^2-8x+( (-8)/(2))^2=57+( (-8)/(2))^2\\\\x^2-8x+16=57+16`

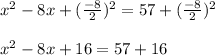
We then factor like a perfect square trinomial and simplify.


`(x-4)^2=73`


`x-4= \pm √(73) \\\\ x = 4+√(73) \ or \ x = 4-√(73)`