Question

Identify the GCF of 10x4y3 − 5x3y2 + 20x2y.

10x2y

10x3y

5x2

5x2y

Answer 1

The GCF, or greatest common factor, is the greatest positive integer that evenly multiplies to make the numbers in the set. For simple numbers, GCF(12, 80, 44) is 4.

The strategy for expressions with variables is still to factor out the greatest term.

For
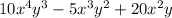
`10x^4y^3-5x^3y^2+20x^2y`, we look for the largest factor in each term.

For
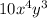
`10x^4y^3`, the largest factors are
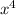
`x^4` and
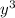
`y^3`. We'll come back to the coefficients in a minute.

For
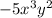
`-5x^3y^2`, the largest factors are
`x^3` and
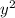
`y^2`. Now, looking back to the previous term and also considering the coefficients, the largest factor of the two is
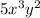
`5x^3y^2`. You could rewrite the first term as
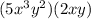
`(5x^3y^2)(2xy)` and the second term as
`-1(5x^3y^2)`.

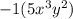
Now, we consider the last term,
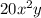
`20x^2y`. The largest factor common to the two other terms is
`5x^2y`.

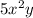
And that's our final answer for the GCF (answer D).

Answer 2

The GCF of the given expression is:

`5x^2y`

Explanation:

The GCF ( greatest common factor ) is the greatest divisor which divides all the terms completely.

Here we have the expression as:

`10x^4y^3-5x^3y^2+20x^2y`

Here we see that the factors of the first term are:

`10x^4y^3=2* 5* x* x* x* x* y* y* y`

The factor of the second term is:

`-5x^3y^2=-1* 5* x* x* x* y* y`

and the factor of the third term is:

`20x^2y=2* 2* 5* x* x* y`

i.e. the factor which is common to all the three terms are:

`5* x* x* y=5x^2y`

Hence, the GCF is:
`5x^2y`