Question

Can someone help me please, how to add this? Thank you!

Answer 1

Answer:
Choice B)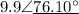
`9.9 \angle \underline{76.10^(\circ)}`

============================================

Step-by-step explanation:

The given vectors in polar form are
(17,60)
(8,220)
by polar form I mean (r,theta) where
r = magnitude
theta = angle

Convert the polar form (r,theta) = (17,60) to component form
x = r*cos(theta)
x = 17*cos(60)
x = 8.5
y = r*sin(theta)
y = 17*sin(60)
y = 14.72243186
The component form of the first vector is (x,y) = (8.5, 14.72243186)

Do the same for the second vector
x = r*cos(theta)
x = 8*cos(220)
x = -6.1283555
y = r*sin(theta)
y = 8*sin(220)
y = -5.1423009
The component form of the second vector is (x,y) = (-6.1283555, -5.1423009)

Now we add the vectors. Add up the corresponding components
(8.5, 14.72243186)+(-6.1283555, -5.1423009)
(8.5+(-6.1283555) , 14.72243186+(-5.1423009))
(2.3716445, 9.58013096)

So,
(x,y) = (2.3716445, 9.58013096)
is the component form of the resultant vector. Its the vector we get after adding the two original vectors

The last step is to convert this back to polar form
r = sqrt(x^2+y^2)
r = sqrt(2.3716445^2+9.58013096^2)
r = 9.869326564
which is roughly 9.9

theta = arctan(y/x)
theta = arctan(9.58013096/2.3716445)
theta = 76.09548164
which rounds to 76.10

So we end up with (r,theta) = (9.9, 76.10) pointing to choice B as the answer