Question

DE has endpoints D 0, 3 and E 0, 12 find the length of DE to the nearest tenth

Answer 1

The answer is 9 because the distance formula is square root of (x2-x1)^2 + (y2-y2)^2

Answer 2

Answer: The length of side DE is 9 units.

Step-by-step explanation: Given that the co-ordinates of the end-points of DE are D(0, 3) and E(0, 12).

We are to find the length RT of the polygon.

We know that

the length of a line segment with endpoints P(a, b) and Q(c, d) is equal to the distance between the points P and Q.

By distance formula, the distance between P(a, b) and Q(c, d) is

`D=√((c-a)^2+(d-b)^2).`

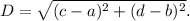
So, the distance between D(0, 3) and E(0, 12) is given by

`DE=√((0-0)^2+(12-3)^2)=√(9^2)=9.`

Thus, the required length of DE is 9 units.