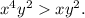Question

Choose the polynomial that is written in standard form. (1 point)

−3x5y2 + 4x3y + 10x2

−8xy2 + 4x4y2 + 3x3

x4y2 + 4x3y5 + 10x4

x6y2 + 4x3y8 + 10x7

Answer 1

Standard form is where the degree of each monomial decreases from left to right. Degree can be found by adding the exponents on each variable.

The only one where this is true is the first one.
The degree goes from 7 to 4 to 2

Answer 2

`-3x^5y^2+4x^3y+10x^2`

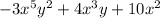
Explanation:

A polynomial in two variables is in standard form if its monomial from left to right are arrangerd in descending order. We say that a monomial
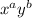`x^ay^b` is greater than a monomial
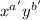`x^{a^(\prime)}y^{b^(\prime)}` if
`a+b > a^(\prime) + b^(\prime)` or
`a+b=a^(\prime)+b^(\prime) \quad \text{and} \quad (a,b)>(a^(\prime),b^(\prime)})` in the alphabetical order.

For example

`x^2y>xy \quad \text{since} \quad 2+1>1+1 \\\\x^2y>xy^2 \quad \text{since} \quad 2+1=1+2 \quad \text{and} \quad 2>1`

The polynomial
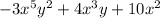`-3x^5y^2+4x^3y+10x^2` is in standard form, since
`x^5y^2 > x^3y >x^2`. On the other hand, the polynomial
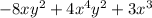`-8xy^2+4x^4y^2+3x^3` is not in standard form since
`x^4y^2>xy^2.`