Question

Solve the proportion

`(3)/(4) = (x)/(6)`

Answer 1

To solve a problem like this, you can use a method called cross-multiplying. This is when you multiply the denominator of the first fraction by the numerator of the other and then multiply the two remaining numbers.


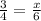
`(3)/(4) = (x)/(6)` Multiply 3 by 6 and multiply 4 by x.
4x = 18 Divide by 4.
x =
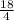
`(18)/(4)` Simplify!
x =
`(9)/(2)`

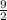
You can check this by comparing the fractions with
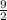
`(9)/(2)` in the place of x.


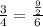
`(3)/(4) = ( (9)/(2) )/(6)` Divide
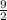
`(9)/(2)` by 6 (
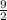
`(9)/(2)` times
`(1)/(6)`).

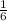
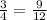
`(3)/(4) = (9)/(12)` Simplify!

`(3)/(4) = (3)/(4)`

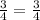
The fractions are equal, so x =
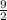
`(9)/(2)` .