Question

What is the simplest form of root 3.025

Answer 1

Answer: √3025

Step-by-step explanation:

1) By convention if you do not mention the index of the root it is square root.

2) By definition the square root of a number x is the numberwhose square is the original number, i.e.

√3025 = 55 because 55^2 = 3025.

3) 3025 is a perfect square because it is the square of a whole numbe.

4) It is easy to find the square root of a perfect square, but if the number is not easily reknownm as a perfect square you will have to probe with several numbers until finding the square root.

For example, you might easily realize that 50^2 is 2500, and that 60^2 is 3600, so you start testing numbers greater thatn 50 and less than 60 until you get 55^2 = 3025.

5) How can you simplify a radical? If you know the properties of radicals you can simplify a radical easily.

You start by decomposing 3025 into its prime factors.

That will result into:


`3025 =5^2{11}^2`

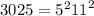
Then, by radical properties:


`\sqrt{5^2{11}^2} = √(5^2) \sqrt{{11}^2} =(5)(11)=(55)`

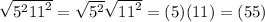
So, the simplest form of √3025 is 55.