Question

What are the values of x and y?

a) x= 136/15, y= 17/15
b) x= 64/15, y= 17/15
c) x= 8/15, y= 136/15
d) x= 64/15, y= 136/15

Answer 1

In the given figure, we have two right angled triangles:
1) Triangle ABC
2) Triangle CDB

Using pythagorean theorem, we can write equations for both triangles.

For triangle ABC:


`(15+x)^(2)= 17^(2)+ y^(2)`

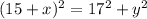
For triangle CDB:


`y^(2)= 8^(2)+ x^(2)`

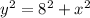
Using the value of y² in the first equation, we get:


`(15+x)^(2)= 289 + 64 + x^(2) \\ \\ 225+30x+ x^(2) =353 + x^(2) \\ \\ 30x=128 \\ \\ x= (128)/(30) \\ \\ x= (64)/(15)`


`y^(2)= 8^(2)+ x^(2) \\ \\ y^(2)=64+ ( (64)/(15) )^(2) \\ \\ y^(2)= (18496)/(25) \\ \\ y= (136)/(15)`

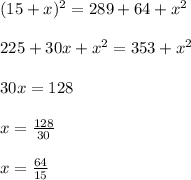
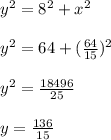
Thus the d option gives the correct values of x and y