Question

A rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find the time that the rocket will hit the ground, to the nearest 100th of second.

y
=
−
16
x
2
+
170
x
+
61

Answer 1

10.97 seconds

Explanation:

You want to know when a rocket will hit the ground if its height is given by y = -16x² +170x +61, where x is seconds after launch.

Quadratic Formula

The formula for the solutions of a quadratic equation is ...

`\text{for }ax^2+bx+c=0\\\\x=(-b\pm√(b^2-4ac))/(2a)`

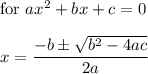
When we apply this to the equation y=0, we have ...

`x=(-170\pm√(170^2-4(-16)(61)))/(2(-16))=(170\pm√(32804))/(32)\\\\x\approx 10.97\quad\text{seconds}`

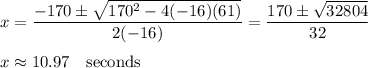
The rocket will hit the ground after about 10.97 seconds.

<95141404393>