Question

To the nearest hundredth, what is the length of line segment AB ? Drag your answer into the box. The length of line segment AB is approximately units

9.54
10.44
13.00
13.15

Answer 1

I'm a nooby so 10.44.

Explanation:

Answer 2

B. 10.44 units.

Explanation:

We are asked to find the length of line segment AB.

To find the length of line segment AB we will use distance formula.

`\text{Distance}=√((x_2-x_1)^2+(y_2-y_1)^2)`

Upon substituting the coordinates of point A and B in distance formula we will get,

`\text{Distance between point A and point B}=√((1--9)^2+(-1--4)^2)`

`\text{Distance between point A and point B}=√((1+9)^2+(-1+4)^2)`

`\text{Distance between point A and point B}=√((10)^2+(3)^2)`

`\text{Distance between point A and point B}=√(100+9)`

`\text{Distance between point A and point B}=√(109)`

`\text{Distance between point A and point B}=10.4403065089105502\approx 10.44`

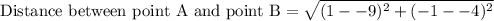
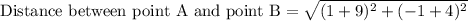
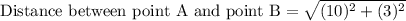
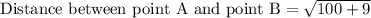
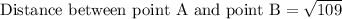
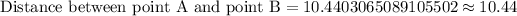
Therefore, the length of line segment AB is 10.44 units and option B is the correct choice.