Question

Maria wrote the equation log(x/2)+log(20/x^2)=log8. What is the solution to Maria's equation?

a. x=3/10
b. x=4/5
c. x=5/4
d. x10/3

Answer 1

C. x=5/4

Explanation:

Correct answer on edge 2022

Answer 2

The solution is x=5/4.

We use the properties of logs to rewrite the equation:

`\log[((x)/(2))((20)/(x^2))]=\log8 \\ \\\log((20x)/(2x^2))=\log8 \\ \\\log((10)/(x))=\log8`

Get all of the logs on the same side of the equation y subtracting log 8:

`\log((10)/(x))-\log8=\log8 - \log8 \\ \\\log((10)/(x))-\log8=0`

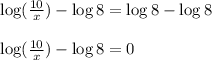
Use the properties of logs to rewrite:

`\log((10)/(x)/8)=0 \\ \\\log((10)/(x)/(8)/(1))=0 \\ \\\log((10)/(x)*(1)/(8))=0 \\ \\\log((10)/(8x))=0`

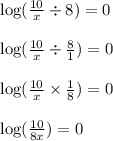
Exponentiate:

`10^0=(10)/(8x) \\ \\1=(10)/(8x)`

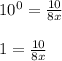
Multiply both sides by 8x:
1*8x = (10/8x)*8x
8x=10

Divide both sides by 8:
8x/8 = 10/8
x = 10/8 = 5/4