Question

from a point on the ground 47 feet from the foot of a tree, the angle of evelation of the top of the tree is 35 degrees. find the height of the tree to the nearest foot

Answer 1

The height of the tree is 32.90 feet.

P is the point on the ground, T is the top of the tree, and h is the height of the tree. We are given that PT = 47 feet and the angle of elevation from P to T is 35 degrees.

We want to find the height of the tree, which is represented by h in the diagram. We can use the tangent function to solve for h.

The tangent of an angle is defined as the ratio of the opposite side to the adjacent side in a right triangle.

In this case, the opposite side is h and the adjacent side is PT = 47 feet. Therefore, we have

tan(35°) = h/47

Solving for h, we get:

h = 47 * tan(35°) ≈ 32.90 feet

Rounding to the nearest foot, we find that the height of the tree is 33 feet.

Answer 2

For a better understanding of the solution provided here please go through the diagram in the attached file.

In the diagram, F is the foot of the tree.

T is the top of the tree. Then TF will be the height of the tree.

P is the point on the ground 47 feet from the foot of a tree. Therefore, PF=47.

Now, we know that the tree grows vertical from the ground and thus
`\angle F=90^(\circ)`

Thus, the triangle
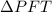`\Delta PFT` is a right triangle.

Now, we can apply the trigonometric ratio, tan in this triangle as:

`tan(\angle P)=(Perpendicular)/(Base) =(TP)/(PF)`

`\therefore tan(35^(\circ))=(TF)/(47)`

`TF=47* tan(35^(\circ))\approx32.91\approx33`

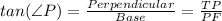
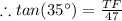
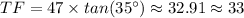
Thus, the the height of the tree to the nearest foot is 33 feet.