Answer:
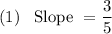
(2) Equation of line in slope-intercept form is
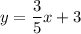
(3) Equation of line in standard form is:
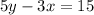
Explanation:
Equation of a line in slope-intercept form is
y = mx + b
where m = slope and b = y-intercept
Slope =
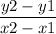
where (x1, y1) and (x2, y2) are two points on the line.
y2 - y1 is known as the rise
x2 - x1 is known as the run
Slope is also defined as rise/run
We are given x-intercept = -5.
The ex-intercept is the point at which the line crosses the x-axis. At this point the y-value = 0.
So we get one of the points (-5, 0)
We are given y-intercept = 3
The y-intercept is the point at which the line crosses the y-axis. At this point the x-value is 0
So another point on the line is (0, 3)
Knowing this we can compute rise and run
rise = y2 - y1 = 3 - 0 = 3
run = x2 - x1 = 0 - (-5) = 0+5 = 5
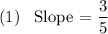
(2) Equation is
y = mx + b where m = slope and b = y-intercept
Slope = 3/5 from (1) and y-intercept = 3
So equation of line in slope-intercept form is
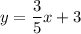
(3) Equation in standard form
In (2) subtract (3/5)x from both sides.

We can multiply both sides by 5 to get
