1 Answer

Sachin G S · Answer 1 · 2019-02-28T16:54:41+0000

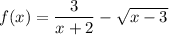
$f(x)=\frac3{x+2}-√(x-3)$

Two immediate observations:

(1) Clearly, we can't have
x=-2

, since that would make both the rational and the square root terms undefined.

(2) If

is real, then
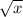
$\sqrt x$ only exists if
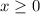
$x\ge0$ . This means that for
√(x-3)

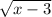
to exist, we require
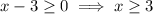
$x-3\ge0\implies x\ge3$ .

If
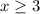
$x\ge3$ , then we don't have to worry about

ever taking on a value of -2.

Please log in or register to add a comment.