Answer:
Explanation:
Lets name the perpendicular drawn from vertex to opposite side " h " for calculation purposes (Refer the figure attached)
so first in the triangle ABC,
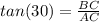
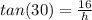
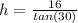
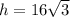
Now refer the triangle ACD , there we can use the trigonometric ratio
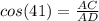
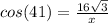
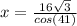
x= 36.7