Question

The numerator and denominator of a fraction are in the ratio of 3 to 5. If the numerator and denominator are both decreased by 2, the fraction is now equal to .

If n = the numerator and d = the denominator, which of the following systems of equations could be used to solve the problem?

5n = 3d and n - 2 = 2d - 4
5n = 3d and 2n - 4 = d - 2
3n = 5d and 2n - 4 = d - 2

Answer 1

A 5n=3d and n-2=2d-4

Explanation:

Answer 2

You probably missed that when the numerator and denominator are both decreased by 2, the new fraction is now equal to 1/2.

The numerator of the fraction is "n" and the denominator of the fractions is "d". Initially the numerator and denominator are in the ratio 3 to 5. In equation form we can state this as:


`n:d=3:5 \\ \\ (n)/(d)= (3)/(5) \\ \\ 5n=3d`

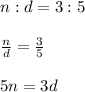
When both numerator and denominator are decreased by 2, the new numerator will be n-2 and denominator will be d-2. These numerator and denominators are in ratio 1 to 2. In equation form we can write this as:


`n-2:d-2=1:2 \\ \\ (n-2)/(d-2) = (1)/(2) \\ \\ 2(n-2)=1(d-2) \\ \\ 2n-4=d-2`

This is our second equation. Thus the two equation which can be used to solve the problem are:

5n = 3d
and
2n - 4 = d - 2