Question

Point A is located at (0, 4) and point B is located at (−2, −3). Find the x value for the point that is 1/4 the distance from point A to point B.

−1

−0.75

−0.5

−0.25,

Answer 1

- First thing, find the distance between A and B:

AB =
`\sqrt{( x_(2) - x_(1))^(2) + ( y_(2) - y_(1))^(2) }` =
=
`\sqrt{(0-(-2))^(2) + (4-(-3))^(2) }` =
=
`√(4+49)` =
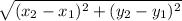
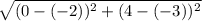
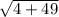
= √53

- Hence, we know that the distance between point A and the point C to be found is:
AC = √53 / 4

- The only other thing we know about point C is that it lays on the line that connects A and B. Let's use the point-slope formula to find the equation of this line:

y - y₂ =
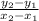
`(y_(2) - y_(1) )/(x_(2) - x_(1) )` (x - x₂)
y - (-3) = (7/2)(x - (-2))
y + 3 = (7/2)(x + 2)
y = (7/2)x + 7 - 3
y = (7/2)x + 4

This is the equation that ties the coordinates of every point laying on it, therefore it is vaid for A, B and, above all, C which will be:
C (x , (7/2)x + 4)

- Now let's find the distnce between A and C:
AC =
`\sqrt{( x_(2) - x_(1))^(2) + ( y_(2) - y_(1))^(2) }`=
=
`\sqrt{(x-0)^(2) + ((7/2)x+4-4)^(2) }` =
=
`\sqrt{x^(2) + (49/4)x^(2) }` =
=
`\sqrt{(53/4) x^(2) }` =
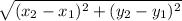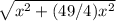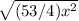=+/-(√53/2)x
- Lastly, we know this distance must be equal to √53 / 4, therefore you need to set and solve the equation:
+/-(√53/2)x = √53 / 4
(1/2)x = +/-(1/4)
x = +/-(1/2)

Since point C is towards point B, we have to take the negative answer:
x = -(1/2)

- Therefore the correct answer is C: -0.5