Your ellipse is given in the form:
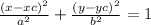
Indeed, you have:
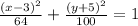
Therefore you can easily find:
a) the coordinates of the center:
in your case xc = 3 and yc = -5
hence C(3 , -5)
b) lenght of the major and minor axis:
in your case a² < b²:
a² = 64 ⇒ a = 8 (ATTENTION! This is the
semi-minor axis)
b² = 100 ⇒ b = 10 (again, this is the
semi-major axis)
Therefore,
minor axis 2a = 16 and major axis 2b = 20
c) coordinates of the foci:
Since you have a² < b², foci have the generic coordinates F₁₂ (xc , yc+/-c)
where c = √(b² - a²)
Let's compute c = √(100 - 64) = √36 = 6
yf₁ = -5 - 6 = -11
yf₂ = -5 + 6 = -1
Therefore:
F₁ (3, -11) and F₂(3, +1)
d) the graph is in the picture attached