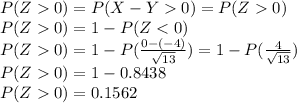Answer:
0.1562
Explanation:
Step 1
In this tep we define the normal distributions in this problem. . The lifetime of the Duracell battery is a normal random variable X with parameters (10,4). The lifetime of the Infinitycell battery is a normal random variable with parameters (14.9).
Step 2
Define the new normal distribution formed by the combination of these two distributions. We define a random variable Z such that
,
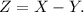
This will be a random variable with mean of
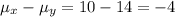 . This random variable will have a variance of
. This random variable will have a variance of
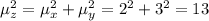 . The mean for this distribution is
. The mean for this distribution is
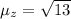 . The random variable Z is normally distributed with parameters (-4,13)
. The random variable Z is normally distributed with parameters (-4,13)
Step 3
The next step is to calculate the probability that
 . For that we perform the calculation shown below. Along the way , we will use the method of transforming any normal distribution to the standard normal distribution.This transformation is
. For that we perform the calculation shown below. Along the way , we will use the method of transforming any normal distribution to the standard normal distribution.This transformation is
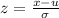 .
.