Here we have to calculate the pressure difference between two ends of the tube.
The diametre of tube [d] =1.90 mm
we know that 1 mm=
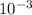
The radius of tube [r]=0.95 mm i.e 0.00095 m
The length of the tube [l]=9.40 cm i.e 0.0940 m
The coefficient of visocity of the oil
![[\eta]](https://img.qammunity.org/2019/formulas/physics/high-school/c8kuumr6nw3v2ih5i8y4ub41oj151r4dga.png) =0.20 pa.s
=0.20 pa.s
The rate of flow of oil
![[(dv)/(dt) ]=6.4mL/min](https://img.qammunity.org/2019/formulas/physics/high-school/w5ggy0ojkgi0f0sepj0o7dw0b0vv6kxob9.png)
we know that 1 mL=
 [1L=
[1L=
![10^(-3) m^(3) ]](https://img.qammunity.org/2019/formulas/physics/high-school/3dt4f3ztfy6w91tj96ooh47j24wisrauua.png)
Hence 6.4mL/m^3=
 m^3/s
m^3/s
we know that
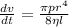
Hence
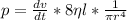
⇒
![p=1.067*10^(-7) *8*0.20*0.0940 *(1)/( 3.14*[0.00095]^4)](https://img.qammunity.org/2019/formulas/physics/high-school/393sa5togaaemf0x8t6vzbi6tey68v8fx8.png) pa
pa
⇒ P=6.274630973*
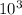 pa
pa