Question

Calculate the total force on the Earth due to Venus, Jupiter, and Saturn, assuming all four planets are in a line. The masses are Mv=0.815ME, MJ=318ME, Msat=95.1ME, Msun=1.99x10^30kg, ME=5.98x10^24kg and the mean distances of the four planets from the Sun are 108, 150, 778, and 1430 million km. Apparently the answer is 9.56x10^17 N but I'm not sure how to get to that .-.,

Answer 1

Answer: Total Force =
`9.56*10^(17)`

Step-by-step explanation:

Line points are: Sun - Venus - Earth - Jupiter - Saturn

Newton's law of universal gravitation states that every particle attracts every other particle in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This means:

`F=G(m_(1) m_(2))/(r^(2) )`

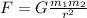
Where,

G is the gravitational constant,

m1 and m2 are the masses of the objects,

and r is the distance between the centers of their masses.

So, if G value is
`6.674*10^(-11)  [(m^(3))/(kg*s^(2))]`, then we replace the equation with the corresponding values:

`F=6.674*10^(-11) (-(0.815ME^(2))/((4.2*10^(10))^(2)) + (318ME^(2))/((6.28*10^(11))^(2)) + (95.1ME^(2))/((1.28*10^(12))^(2)))`

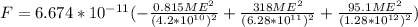
To get the distances we subtract the distances between the sun and earth and the distances between the other planets and the sun.

Answer 2

You need to consider the following:
Me (mass of Earth) = 5.98 x 10^24 kg
Ms (mass of Sun) = 1.99 x 10^30 kg
G = 6.67 x 10^-11 N

Formula:
F = G * M1M2/r^2
The ratio FT/F = 4.02x10^-4 / 14.8
= 2.72x10^-5

Since,
1/2.72x10^-5 = 36800
The fraction ratio is 1/36800
= 9.56x10^17 N