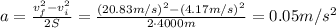Question

a bicyclist in the Tour De France crests a mountain pass as he moves at 15km/h. At the bottom 4km/h farther, his speed is 75km/h. What is his average acceleration(m/s^2) while riding down the mountain?,

Answer 1

For an uniformly accelerated motion, the following relationship can be used:

`2aS = v_f^2 -v_i^2`
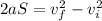
where a is the acceleration, S the distance covered, vf the final speed and vi the initial speed.

Before using the formula, we need to convert everything into SI units.
The distance covered is:

`S=4 km=4000 m`
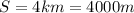
To convert the speed from km/h to m/s, let's keep in mind that

`1 km=1000 m`

`1h=3600 s`
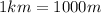
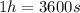
so

`1 (km)/(h)= (1000 m)/(3600 s)= (1)/(3.6)`
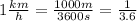
is the conversion factor.
So the speeds are:

`v_i = 15 km/h \cdot (1)/(3.6)=4.17 m/s`

`v_f = 75 km/h \cdot (1)/(3.6)=20.83 m/s`

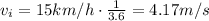
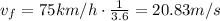
and so, now we can re-arrange the formula to find a, the average acceleration:

`a= (v_f^2-v_i^2)/(2S) = ((20.83m/s)^2-(4.17m/s)^2)/(2\cdot 4000 m)=0.05 m/s^2`