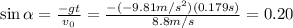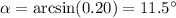Question

A soccer ball is kicked with an initial speed of 8.8 m/s. After 0.179 s it is at its highest point. What was its initial direction of motion?,

Answer 1

To solve the problem we can consider only the motion on the vertical direction (y-axis). Let's the take upward as positive direction, such that the acceleration of the motion (the gravitational acceleration) is negative:
`g=-9.81 m/s^2`, because it is against the direction of the motion.
The initial speed of the ball on the y-axis is
`v_0 \sin \alpha`, where
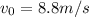
`v_0 = 8.8 m/s` and where
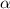
`\alpha` is the angle of the initial velocity v0 with respect to the horizontal, so it's the direction that we want to find.

The law of the velocity on the y-axis is:

`v(t)=v_0 \sin \alpha + gt`
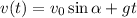
Where t is the time. At its highest point, the vertical velocity of the ball is zero, and this occurs when t=0.179 s:
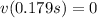
`v(0.179 s)=0`. So we can write:

`v(0.179 s)=v_0 \sin \alpha + gt=0`
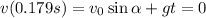
And substituting the numbers we can find the value of the angle:

`\sin \alpha = (-gt)/(v_0)= (-(-9.81 m/s^2)(0.179 s))/(8.8 m/s)=0.20`

`\alpha = \arcsin (0.20)=11.5 ^(\circ)`