Question

The function h(t) = -2 (t-3)^2 +23 represents the height in feet, t seconds after a volleyball is served which of the following statements are correct

A. the volleyball reached it's maximum height of 3 sec
B. The maximum height of the vollybal was 23 ft
C. If the vball is not returned by the opposing team it will hit the ground in 5.5 sec
D. The graph that models the volleyball height over time is exponential
E. The vball was served from a height of 5 ft

Answer 1

A) The volleyball reached its maximum height after 3 seconds.
b) The maximum height of the volleyball was 23 feet.
e) The volleyball was served for a height of 5 feet.

Answer 2

A. the volleyball reached it's maximum height of 3 sec

B. The maximum height of the vollybal was 23 ft

E. The vball was served from a height of 5 ft

Explanation:

h(t) = -2 (t-3)^2 +23

Given equation is in the form of
`f(x)= a(x-h)^2 + k`

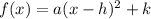
(h,k) is the vertex

Now we compare f(x) with h(t)

h(t) = -2 (t-3)^2 +23

h = 3 and k = 23

Vertex is (3,23)

h=3 . this means the volleyball reaches its maximum height in 3 seconds

k = 23. this means the volleyball reaches the maximum height of 23 ft

When ball reaches the ground the height becomes 0. so plug in 0 for h(t) and solve for t

0= -2 (t-3)^2 +23

Subtract 23 on both sides

-23 = -2(t-3)^2

Divide both sides by -2

`(-23)/(-2) = (t-3)^2`

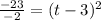
Take square root on both sides

`+-\sqrt{(23)/(2)}= t-3`

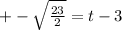
Add 3 on both sides

`+-\sqrt{(23)/(2)}+3= t`

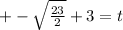
We will get two value for t

t=-0.39 and t= 6.39

So option C is not correct

Given h(t) is a quadratic function not exponential

To find initial height we plug in 0 for x and find out h(0)

h(0) = -2 (0-3)^2 +23 = -2(-3)^2 + 23= -18+ 23= 5

The volleyball was served from a height of 5 ft