Question

PLEASE HELP

y= -2x^2+4x

Direction of opening
Equation of the axis of symmetry (x =___)
Coordinates of the vertex (x,y)
y-intercept (y=_)
Zeroes (if it has 2,1 or no zeroes)
maximum or minimum (y=_)

Answer 1

see explanation

Explanation:

given a quadratic in standard form

y = ax² + bx + c (a ≠ 0 )

• if a > o then curve opens up

• if a < 0 then curve opens down

for y = - 2x² + 4x ← in standard form with a = - 2, b = 4 and c = 0

here a = - 2 < 0 so curve opens down

-------------------------------------------------

the axis of symmetry is a vertical line passing through the vertex

the x- coordinate of the vertex, which is also the equation of the axis of symmetry is

x = -
`(b)/(2a)` = -
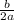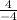`(4)/(-4)` = 1

equation of axis of symmetry is x = 1

substitute x = 1 into the equation for y- coordinate of vertex

y = - 2(1)² + 4(1) = - 2 + 4 = 2

vertex = (1, 2 )

-----------------------------------------------------

to find the zeros let y = o , that is

- 2x² + 4x = 0 ← factor out - 2x from each term

- 2x(x - 2) = 0

equate each factor to zero and solve for x

- 2x = 0 ⇒ x = 0

x - 2 = 0 ⇒ x = 2

the zeros are x = 0 and x = 2

-----------------------------------------------------------

since the graph opens down then it has a maximum value

this is the y- coordinate of the vertex

thus maximum at y = 2

Answer 2

Vertex: (1, 2)
AOS: x = 1
Y - intercept: (0 ,0)
Zeros: 0, 2
Maximum