Question

Your boss tells you that she needs a decision by the end of the day about the machine you want to purchase for your new operation. You have four options, and your boss reminds you to be as cost-efficient as possible but that she also wants the best efficiency. Which is your best option?

Option 1: This $5,000 machine is supplied energy at a rate of 1,900 W and does useful work at a rate of 1,786 W.
Option 2: This $4,500 machine is supplied energy at a rate of 1,450 W and does useful work at a rate of 1,300 W.
Option 3: This $4,750 machine is supplied energy at a rate of 1950 W and does useful work at a rate of 1833 W.
Option 4: This $4,750 machine is supplied energy at a rate of 2,000 W and does useful work at a rate of 1,822 W.

A. Option 1 B. Option 2
C. Option 3 D. Option 4

Answer 1

Option (I) has the lowest energy rate so that would be best option.

Step-by-step explanation:

(I). Given that,

Input energy = 1900 W

Output energy = 1786 W

We calculate the loss of energy

Using formula of loss of energy

`E_(loss)= E_(in) - E_(out)`

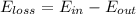
Put the value into the formula

`E_(loss)=1900-1786= 114\ W`

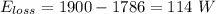
(II). Given that,

Input energy = 1450 W

Output energy = 1300 W

We calculate the loss of energy

`E_(loss)=1450-1300= 150\ W`

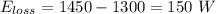
(III). Given that,

Input energy = 1950 W

Output energy = 1833 W

We calculate the loss of energy

`E_(loss)=1950-1833= 117\ W`

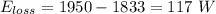
(IV). Given that,

Input energy = 2000 W

Output energy = 1822 W

We calculate the loss of energy

`E_(loss)=2000-1822= 178\ W`

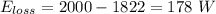
Hence, Option (I) has the lowest energy rate so that would be best option.

Answer 2

Option 1 : 1900 - 1786 = 114

Option 2 : 1450 - 1300 = 150

Option 3: 1950 - 1833 = 117

Option 4: 2000 - 1822 = 178


Option 1 has the lowest energy rate so ver time would be the best deal.