ANSWER

Step-by-step explanation
The sum of the interior angles of the given triangle is
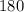
This implies that
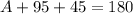
We group like terms to get,
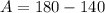
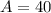
The law of sines is given by,
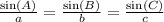
Based on our known values, we use,
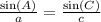
We now substitute the values to get,
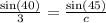
We reciprocate both sides of the equation to get,
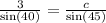
We now multiply both sides by
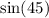
to get,
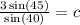
or

The correct answer is B.