Answer: option B. 2d^2 + 14d + 16
----------------------------
(d+8)(d-8)
Step-by-step explanation:The question is:
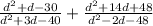
1) Start factoring all the polynomials to rewrite the fractions.
2) d^2 + d - 30 = (d + 6)(d - 6)
3) d^2 + 3d - 40 = (d + 8)(d - 5)
4) d^2 + 14d + 48 = (d + 6) (d + 8)
5) d^2 - 2d - 48 = (d - 8)(d + 6)
6) rewrite the fractions:
(d+6)(d-5) (d+8)(d+6)
----------------- + -----------------
(d+8)(d-5) (d-8)(d+6)
7) simplify the fractions cancelling the factors that are equal in the numerator and the denominator:
d+6 d+8
-------- + -------
d+8 d-8
8) take least common denominatior: (d+8)(d-8), and sum the fractions:
(d-8)(d+6) + (d+8)^2
--------------------------------
(d+8)(d-8)
9) expand the parenthesis in the numerator and combine like terms:
d^2 - 2d - 48 + d^2 + 16d + 64
------------------------------------------- =
(d+8)(d-8)
2d^2 + 14d + 16
= ----------------------------
(d+8)(d-8)
And that is the option B.