Question

The quadratic equation y = 2(x – 2)2 + 2 with no real solution is graphed. Which value of k will change the function to one with exactly one solution?

Answer 1

Answer: 0 ZERO

Explanation:

Answer 2

On the attached diagram red curve is the graph of the quadratic function
`y = 2(x - 2)^2 + 2.` As you can see this graph has no intersections with x-axis, this means that there are no solutions.

If you translate red curve 2 units down, you obtaine the graph (blue curve) of the function
`y = 2(x - 2)^2` and this graph has one common point with x-axis. This means that there will be exactly one solution.

Answer: k=-2 (you add -2 to the function
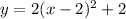`y = 2(x - 2)^2 + 2` to obtain the function
`y = 2(x - 2)^2`).