We have to prove that
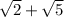 is irrational. We can prove this statement by contradiction.
is irrational. We can prove this statement by contradiction.
Let us assume that
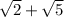 is a rational number. Therefore, we can express:
is a rational number. Therefore, we can express:

Let us represent this equation as:
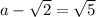
Upon squaring both the sides:
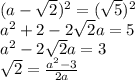
Since a has been assumed to be rational, therefore,
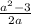 must as well be rational.
must as well be rational.
But we know that
 is irrational, therefore, from equation
is irrational, therefore, from equation
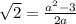 the expression
the expression
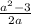 must be irrational, which contradicts with our claim.
must be irrational, which contradicts with our claim.
Therefore, by contradiction,
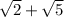 is irrational.
is irrational.