Question

Find the area of a sector with a central angle of 2pi/15 and a radius of 18.8 m

Answer 1

74.02 square meters.

Explanation:

We are asked to find the area of sector of circle, whose central angle is
`(2\pi)/(15)`.

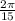We will use area of sector formula to solve our given problem.

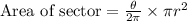`\text{Area of sector}=(\theta)/(2\pi)* \pi r^2`, where, r represents radius of circle.

Upon substituting our given values in above formula, we will get:

`\text{Area of sector}=((2\pi)/(15))/(2\pi)* \pi (18.8)^2`

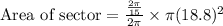
Using fraction rule
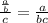`((a)/(b))/(c)=(a)/(bc)`, we will get:

`\text{Area of sector}=(2\pi)/(15* 2\pi)* \pi (18.8)^2`

`\text{Area of sector}=(1)/(15)* \pi * 353.44`

`\text{Area of sector}=23.5626666* \pi`

`\text{Area of sector}=74.0243004\approx 74.02`

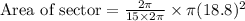
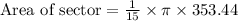
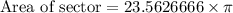
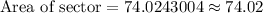
Therefore, the area of given sector of circle is 74.02 square meters.

Answer 2

we know that
[Area of a circumference]=pi*r²
for r=18.8 m
Area=pi*18.8²=1109.80 m²

if the area for 2pi radians (full circumference) is --------------> 1109.80 m²
for 2pi/15----------------------------------> X
X=(2pi/15)*1109.80/2pi----------> 73.99

the answer is 73.99 m²