ANSWER
The given system of equations has no solution.
Step-by-step explanation
We write the two equations in the slope-intercept form,
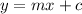
The first equation is
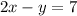
We make y the subject to obtain,
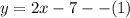
The second equation is already in slope intercept form.
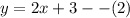
We can see that the two equations have the same slope but different y-intercept. This implies that, the two equations will never intersect. Therefore the system of equations has no solution.