Question

How many 4-sequences on {0..9} do not begin with 0?

Answer 1

I take a
`n`-sequence to mean any permutation of the digits 0-9 of length
`n`. Furthermore, I'm assuming no number can be repeated.

If that's the case, then for any 4-sequence, the first digits place (leftmost) has 9 possible choices (1-9). Once that number is used up, we have 9 numbers left in the pool of digits, from which we select a 3-sequence. The number of possible 3-sequences would be
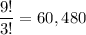
`(9!)/(3!)=60,480`. Multiply this by 9 (to account for the first digit's possibilities) and we get a grand total of
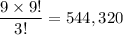
`(9*9!)/(3!)=544,320` possible 4-sequences on
`\{0,\ldots,9\}`.