Question

Find all integer solutions to the pair of congruences (if any) x ≡ 17 (mod 23) 70x ≡ 3 (mod 93).

Answer 1

First, note that
`93=3*31`, which gives


`70x\equiv3\pmod{93}\implies\begin{cases}70x\equiv3\equiv0\pmod3\\70x\equiv3\pmod{31}\end{cases}`

so in fact we're dealing with the system


`\begin{cases}x\equiv17\pmod{23}\\70x\equiv0\pmod3\\70x\equiv3\pmod{31}\end{cases}`

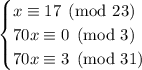
Now, 3, 23, and 31 are relatively prime, so we can use the Chinese remainder theorem. But before we do that, we need to rework and ultimately eliminate the coefficients of
`x`.

From the second equivalence, it follows immediately
`x` is some multiple of 3; this is because
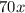
`70x` is divisible by 3, but 3 doesn't divide 70, so it must divide
`x`.

For the third equivalence, we can write
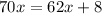
`70x=62x+8`. Then modulo 31, we have that
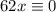
`62x\equiv0`, which leaves us with
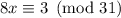
`8x\equiv3\pmod{31}`. We want a congruence of the form
`x\equiv\cdots`, and to get that we can multiply
`8x` and 3 by the inverse of 8 modulo 31.

To find this inverse, we solve for
`y` in the relation


`8y\equiv1\pmod{31}`

by using the Euclidean algorithm, or making just making the observation that
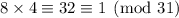
`8*4\equiv32\equiv1\pmod{31}`, so
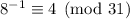
`8^(-1)\equiv4\pmod{31}`. Distributing 4 across the third equivalence in our system gives
`x\equiv4\pmod{31}`.

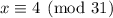
So to recap, we now have


`\begin{cases}x\equiv17\pmod{23}\\x\equiv0\pmod3\\x\equiv12\pmod{31}\end{cases}`

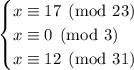
and we're ready to use the CRT.

As a starting point, let's take


`x=(17)+(23)+(23)=63`

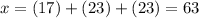
It's clear that taken modulo 23, the latter two terms vanish and we have a remainder of 17, as desired. 63 is already a multiple of 3, but just to avoid doing more work later, let's multiply each term by 3 anyway to keep getting a remainder of 0:


`x=(17*3)+(23*3)+(23*3)=146`

Now multiply the first two terms by 31 to make sure they vanish when taken modulo 31. Meanwhile,
`23*3\equiv69\equiv7\pmod{31}`, but we want to get 12, so we would multiply this term by the inverse of 7 mod 31, and again by 12.

We can make a quick observation that
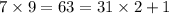
`7*9=63=31*2+1`, so
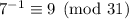
`7^(-1)\equiv9\pmod{31}`. Alternatively, you can use the Euclidean algorithm to find this inverse. Either way, we get


`x=(17*3*31)+(23*3*31)+(23*3*9*12)=11,172`

So we're told that


`x=11,172+(23*3*31)k=11,172+2139k`

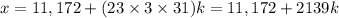
is our solution set, where
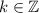
`k\in\mathbb Z`. We can "simplify" this slightly by finding the least positive residue modulo the product of our moduli, which would be


`11,172\equiv477\pmod{2139}`

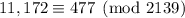
so we end up with


`x=477+2139k`

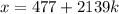
for integers
`k`.